57Fe Paramagnetic Hyperfine Structure (PHS)

Demonstration of concordance of corresponding models of MossWinn with selected literature examples.

Calculation of Mossbauer spectrum model curves accounting for 57Fe paramagnetic hyperfine structure (PHS) of paramagnetic iron ions requires the consideration of the combined effect of the nuclear- and the electronic spin Hamiltonian on the nuclear- and electronic states of the ion. As the latter are influenced by the crystal field the ion is situated in, corresponding terms appear in the combined Hamiltonian. When a powder sample is measured in conjunction with the application of an external magnetic field, the calculation of corresponding Mossbauer spectrum models requires the implementation of a spherical integral over all possible orientations of the external magnetic field with respect to the Hamiltonian reference frame that is considered to be fixed to the individual molecules/crystallites. This spherical integral can in general be carried out only numerically, which makes the calculation of PHS theory based model curves a rather time consuming process for powders. In MossWinn 4.0 57Fe PHS models have been implemented by making use of parallel computing techniques for the calculation of this spherical integral, which can (in comparison with traditional serial algorithms) result in a considerably enhanced calculation speed on today's higher-end multi-core processor based computers. Together with the MossWinn Internet Database and the global search method of MossWinn that may both be especially useful in finding a reasonable starting parameter set for PHS models, the corresponding newly developed routines of MossWinn 4.0 are expected to make the work with 57Fe PHS theories considerably more efficient and less complicated than it was possible before.

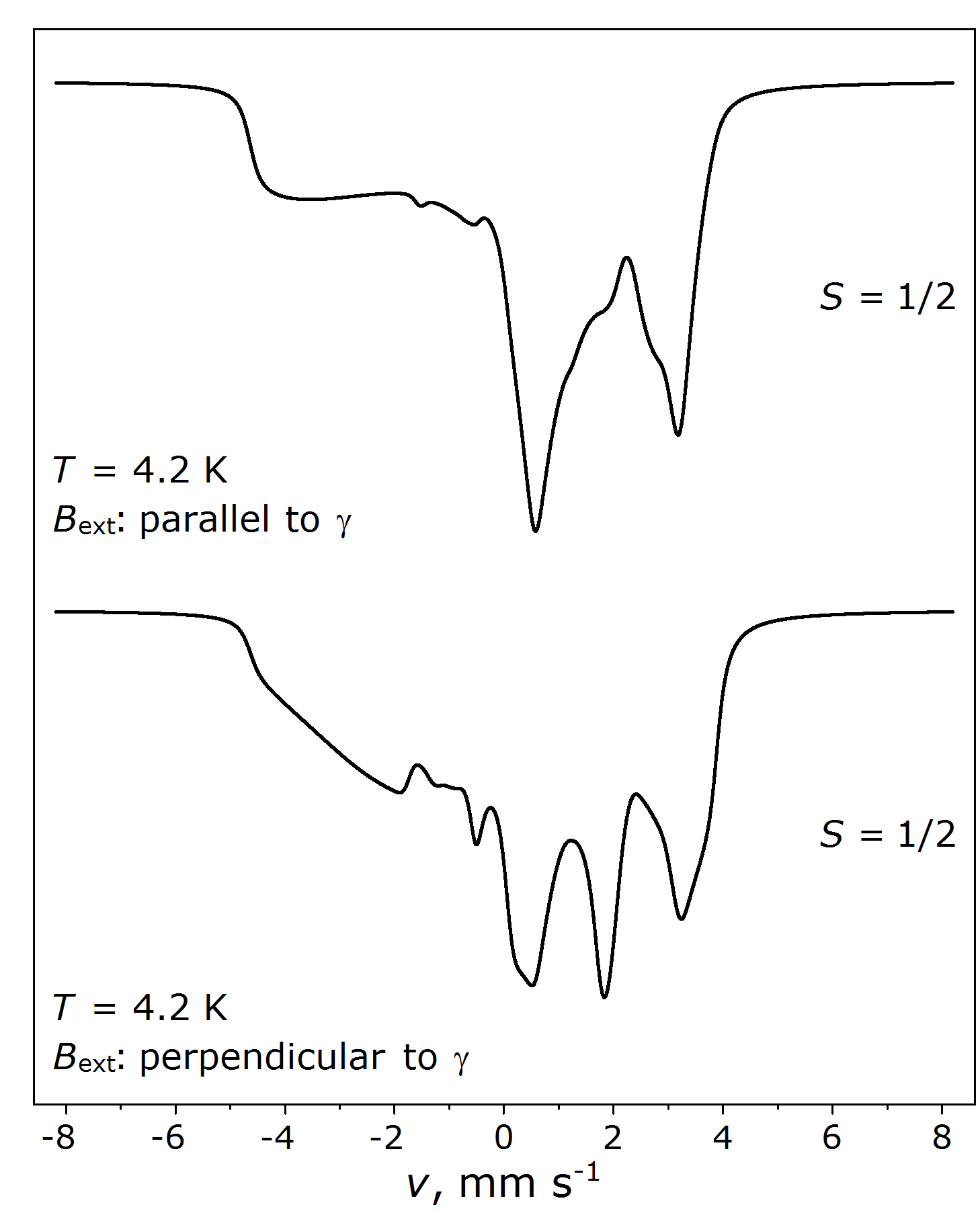
Given the computing power one has available, the calculation of PHS spectrum models in general requires balancing between accuracy and calculation time. Spectrum models calculated according to the same Hamiltonian and associated parameters may depend on one's choice concerning this balance. On account of this potential variability of 57Fe PHS spectra, it appears to be instructive to compare calculations of MossWinn with those in selected literature examples, among others to demonstrate the concordance of MossWinn's calculations with those of earlier works. Such comparisons are given below for different spin states of iron. Parameter values given in the listed literature examples are used to recreate the corresponding PHS model curves in MossWinn with high accuracy. The resulted theoretical curves are then displayed here together with the list of the associated parameters as they should be set in MossWinn. Consult with the referenced papers in order to compare the results produced by MossWinn with the associated curves in the literature. Whenever the referenced work gives a parameter value in a unit different from that default in MossWinn, we also give the conversion factors needed to arrive at the parameter value that should be set in MossWinn.

On the basis of the comparisons given below, the PHS model curves calculated by MossWinn are in general truly concordant with corresponding literature curves. Even in the case of works published as early as in the 1970s usually minor differences can be detected only, which may easily follow from the use of different numerical integration algorithms, as well as from differences concerning the accuracy up to which the curves were calculated. Noteworthy deviations of literature curves from those produced by MossWinn were found in one case (#1), which we also associate with the lower-accuracy numerical integration applied in the work in question. In contrast, the agreement with more recent works (#1, #2, #3) is typically excellent. Among the examples given here, there appears to be a perfect agreement between published model curves and those produced by MossWinn in three non-trivial cases (#1, #2, #3).

The model spectra displayed below can be downloaded as a zipped TPF project group file: link. After extraction of the TPF file from the zip file, in the main menu of MossWinn turn to the menu option MPD → Import Project... to import the spectra from the extracted tpf file.

Note that in order to use the PHS models in MossWinn, one needs to have either a DBM version license, or a Full range/Select/Lite version license along with a subscription to the MossWinn Services.

For a detailed description of the PHS models included in MossWinn see the latest version of the manual.

S = 1/2

See Fig. 4 of J. Chem. Phys. 51 (1969) 3608.

  • In this example the case of low-spin Fe3+ (t2g5, S = 1/2) is treated by assuming an octahedral crystal field. In the above work corresponding theoretical spectra are given among others for the case of zero external magnetic field as well as for that of a moderate-strength external magnetic field being perpendicular to the γ-ray direction. By assuming an isotropic hyperfine magnetic interaction along with slow electronic relaxation, with the relevant and non-zero parameter values being set as given below, the theoretical curves calculated by MossWinn (as shown on the right) appear to be identical with those displayed on Fig. 4 of the above paper.
    Note that in the zero-field case the model PHS 1/2 (Powder, ZERO EMF, Slow R.) can calculate the corresponding curve faster in MossWinn.

    Effective Hamiltonian (S = 1/2)

    μB[gxxBxSx + gyyBySy + gzzBz Sz] + gnμN[AxxS xIx + AyySyIy + AzzSzIz]
    – gnμN[BxIx + ByIy + BzIz]

    Case:

    Zero EMF

    Moderate EMF

    Theory used:

    PHS 1/2 (Powder, EMF, Slow R.)

    (0) EXT. MAGN. FIELD [T]:

    0

    0.5

    (0) EMF PAR (0) / PERP (1):

    1

    (1) ISOMER SHIFT:

    0

    (1) Axx [T]:

    -63.0

    (1) Ayy [T]:

    -63.0

    (1) Azz [T]:

    -63.0

    (1) gxx:

    2.0

    (1) gyy:

    2.0

    (1) gzz:

    2.0

    (1) 2S+1 (multiplicity):

    2

    (1) Accuracy level:

    2

    (1) LINE WIDTH:

    0.6

S = 1/2

See Fig. 1 of Biochemistry 12 (1973) 426.

  • In this example the heme protein chloroperoxidase is studied along with its several complexes. Native chloroperoxidase includes low-spin Fe3+ (t2g5, S = 1/2). By assuming a ligand field potential of orthorhombic symmetry, the 57Fe Mossbauer spectrum of chloroperoxidase measured at 4.2 K in 1300 G external magnetic field oriented either parallel or perpendicular to the γ-ray direction is fitted with S = 1/2 model curves in Fig. 1 of the above article. By assuming slow electronic relaxation, with the relevant and non-zero parameter values being set as given below (see article page 431), the corresponding theoretical curves calculated by MossWinn (as shown on the right) appear to be very close to those displayed on Fig. 1 of the above paper. See also the associated video.

    Conversion factor to be considered in this example

    Vzz / 1021 V m-2 ≈ 6 × ½eQVzz / mm s-1

    Effective Hamiltonian (S = 1/2)

    μB[gxxBxSx + gyyBySy + gzzBz Sz] + gnμN[AxxS xIx + AyySyIy + AzzSzIz] + [eQnVzz/(4I(2I – 1))][3I z2 – I(I+1)+η(Ix2 – Iy2)] – gnμN[BxIx + ByIy + BzIz]

    Case:

    EMF perpendicular to γ

    EMF parallel to γ

    Theory used:

    PHS 1/2 (Powder, EMF, Slow R.)

    (0) TEMPERATURE [K]:

    4.2

    (0) EXT. MAGN. FIELD [T]:

    0.13

    (0) EMF PAR (0) / PERP (1):

    1

    0

    (1) ISOMER SHIFT:

    0

    (1) Vzz (EFG) [10^21 V/m2]:

    8.922

    (1) ETA:

    -2.9

    (1) Axx [T]:

    -49.0

    (1) Ayy [T]:

    7.9

    (1) Azz [T]:

    28.4

    (1) gxx:

    1.84

    (1) gyy:

    2.26

    (1) gzz:

    2.63

    (1) Accuracy level:

    3

    (1) LINE WIDTH:

    0.35

Seff = 1/2 (S = 5/2)

See Fig. 8 of Biochemistry 12 (1973) 426.

  • In this example the fluoride complex of chloroperoxidase is studied at 4.2 K in a 2500 G external magnetic field applied parallel to the γ-ray direction. Iron is present in this complex in the high-spin ferric form (Fe3+, S = 5/2). Due to zero field splitting, at 4.2 K only the lowest Kramers doublet is populated, which is modeled in the above work in the frame of a Seff = 1/2 effective spin Hamiltonian accounting for a ligand field potential of orthorhombic symmetry. By assuming slow electronic relaxation, with the relevant and non-zero parameter values being set as given below (see article Table II), the corresponding theoretical curve calculated by MossWinn (top curve on the right) appears to be quite close to that displayed on Fig. 8 of the above paper. Actually, concerning the amplitude ratio of the inner two peaks, the theoretical curve produced by MossWinn is closer to the measured spectrum data than the model curve shown in Fig. 8 of the above work. Certainly, the same spectrum can also be modeled by considering directly the S = 5/2 electronic spin state (bottom curve on the right). The corresponding parameters are given in the second column of the table below. For D > 10 cm-1 ( ∼ 14.4 K ) the spectral shape is not sensitive to the value of D anymore, in agreement with the expectation that at 4.2 K only the lowest Kramers doublet is populated. The E/D and Axx=Ayy=Azz values, given in the table below, were obtained by fitting the Seff = 1/2 model curve with the S = 5/2 spin Hamiltonian in MossWinn. Note that the above work gives E/D = 0.05 for Chloroperoxidase-F, in good agreement with our result. See also the associated video.

    Conversion factors to be considered in this example

    Vzz / 1021 V m-2 ≈ 6 × ½eQVzz / mm s-1

    D / cm-1 ≈ 0.69503457 × D / K

    Effective Hamiltonian (Seff = 1/2)

    μB[gxxBxSx + gyyBySy + gzzBz Sz] + gnμN[AxxS xIx + AyySyIy + AzzSzIz] + [eQnVzz/(4I(2I – 1))][3I z2 – I(I+1)+η(Ix2 – Iy2)] – gnμN[BxIx + ByIy + BzIz]

    Effective Hamiltonian (S = 5/2)

    μB[gxxBxSx + gyyBySy + gzzBz Sz] + D[Sz2 – S(S + 1)/3 + (E/D)(Sx2 – Sy2)] + gnμN[AxxS xIx + AyySyIy + AzzSzIz] + [eQnVzz/(4I(2I – 1))][3I z2 – I(I+1)+η(Ix2 – Iy2)] – gnμN[BxIx + ByIy + BzIz]

    Case:

    Chloroperoxidase-F (Seff = 1/2)

    Chloroperoxidase-F (S = 5/2)

    Theory used:

    PHS 1/2 (Powder, EMF, Slow R.)

    PHS (Powder, EMF, Slow R.)

    (0) TEMPERATURE [K]:

    4.2

    (0) EXT. MAGN. FIELD [T]:

    0.25

    (0) EMF PAR (0) / PERP (1):

    0

    (1) ISOMER SHIFT:

    0.2

    (1) Vzz (EFG) [10^21 V/m2]:

    6.01

    (1) ETA:

    0.1

    (1) D [1/cm]:

    13.9

    (1) E/D:

    0.0465

    (1) Axx [T]:

    -48.0

    -19.82

    (1) Ayy [T]:

    -70.0

    -19.82

    (1) Azz [T]:

    -19.4

    -19.82

    (1) gxx:

    4.8

    2.0

    (1) gyy:

    7.01

    2.0

    (1) gzz:

    1.94

    2.0

    (1) 2S+1 (multiplicity):

    (2)

    6

    (1) Coupled (0) / Decoupled (1):

    (0)

    1

    (1) Accuracy level:

    2

    3

    (1) LINE WIDTH:

    0.35

S = 1/2

See Fig. 8 on page 185 of Peter G. Debrunner: Enzyme Systems in Richard L. Cohen (ed.): Applications of Mossbauer Spectroscopy - Volume I (Academic Press, New York, 1976).

  • In this example 57Fe Mossbauer spectra of oxidized cytochrome P450 — measured at 4.2 K in a small external magnetic field being either parallel or perpendicular to the γ-ray direction — are presented (with reference to M.P. Sharrock: Thesis, 1973, Univ. of Illinois, Urbana, Illinois). Heme iron in this protein takes on the low-spin ferric state (Fe3+, t2g5, S = 1/2) and the corresponding spectra can be quite well modeled with a S = 1/2 spin Hamiltonian by assuming a ligand field potential of orthorhombic symmetry. By assuming slow electronic relaxation, with the relevant and non-zero parameter values being set as given below (see book page 185), the corresponding theoretical curves calculated by MossWinn (as shown on the right) appear to be quite close to those displayed on Fig. 8 of the above book chapter, though MossWinn produces a smoother model curve in the -2 mm/s ... -4 mm/s velocity interval.

    Conversion factor to be considered in this example

    Vzz / 1021 V m-2 ≈ 6 × ½eQVzz / mm s-1

    Effective Hamiltonian (S = 1/2)

    μB[gxxBxSx + gyyBySy + gzzBz Sz] + gnμN[AxxS xIx + AyySyIy + AzzSzIz] + [eQnVzz/(4I(2I – 1))][3I z2 – I(I+1)+η(Ix2 – Iy2)] – gnμN[BxIx + ByIy + BzIz]

    Case:

    EMF parallel to γ

    EMF perpendicular to γ

    Theory used:

    PHS 1/2 (Powder, EMF, Slow R.)

    (0) TEMPERATURE [K]:

    4.2

    (0) EXT. MAGN. FIELD [T]:

    0.25727

    (0) EMF PAR (0) / PERP (1):

    0

    1

    (1) ISOMER SHIFT:

    0.38

    (1) Vzz (EFG) [10^21 V/m2]:

    11.88

    (1) ETA:

    -1.8

    (1) Axx [T]:

    -45.0

    (1) Ayy [T]:

    10.2

    (1) Azz [T]:

    19.1

    (1) gxx:

    1.91

    (1) gyy:

    2.26

    (1) gzz:

    2.45

    (1) Accuracy level:

    3

    (1) LINE WIDTH:

    0.3

S = 1

See Figs. 1 & 2 of J. Phys. Colloques 40 (1979) C2 534.

  • In this example frozen solutions of heme protein compounds are studied with iron being in the Fe4+ (t2g4, S = 1) electronic state. Two sets of spectra were measured in an external magnetic field (applied parallel to the γ-ray) as a function of temperature, which could be modeled by an axial spin Hamiltonian with S = 1. By assuming fast electronic relaxation, with the relevant and non-zero parameter values being set as given below (see article Table I), the theoretical curves and their temperature dependence as calculated by MossWinn (as shown on the right) appear to agree closely with those displayed on Figs. 1 & 2 of the above paper. Note that the magnetic splitting undergoes a minimum as the temperature is increased, which is due to the combined effect of the external magnetic field and the hyperfine magnetic interaction, as explained by the authors in the above paper.

    Conversion factors to be considered in this example

    Vzz / 1021 V m-2 ≈ 6 × ½eQVzz / mm s-1

    D / cm-1 ≈ 0.69503457 × D / K

    Effective Hamiltonian (S = 1)

    Electronic states: μB[gxxBxSx + gyyBySy + gzzBzSz] + D[Sz2 – S(S + 1)/3]

    Nuclear states: gnμN[Axx<Sx>TIx + Ayy<Sy>TIy + Azz<Sz>TIz] +
    [eQnVzz/(4I(2I – 1))][3I z2 – I(I+1)] – gnμN[BxIx + ByIy + BzIz]

    Sample:

    met Mb - H2O2

    HRP Compound II

    Theory used:

    PHS (Powder, EMF, Decoupled, Fast R.)

    (0) TEMPERATURE [K]:

    as indicated beside the spectra

    (0) EXT. MAGN. FIELD [T]:

    as indicated beside the spectra

    (0) EMF PAR (0) / PERP (1):

    0

    (1) ISOMER SHIFT:

    0.09

    0.03

    (1) Vzz (EFG) [10^21 V/m2]:

    8.58

    9.66

    (1) ETA:

    0.0

    0.0

    (1) D [1/cm]:

    24.32621

    22.24111

    (1) Axx [T]:

    -18.7

    -19.3

    (1) Ayy [T]:

    -18.7

    -19.3

    (1) Azz [T]:

    -2.5

    -6.5

    (1) gxx:

    2.27

    2.25

    (1) gyy:

    2.27

    2.25

    (1) gzz:

    1.98

    1.98

    (1) 2S+1 (multiplicity):

    3

    (1) Coupled (0) / Decoupled (1):

    1

    (1) Accuracy level:

    2

    (1) LINE WIDTH:

    0.3

S = 2

See Figs. 4 & 5 of Biochemistry 14 (1975) 4151.

  • In this example reduced samples of cytochrome P-450 are studied. 57Fe Mossbauer spectra were measured — among others — at 4.2 K in external magnetic fields of 8.6 kG and 25 kG applied parallel to the γ-ray direction. Heme iron is present in this protein in the high-spin ferrous form (Fe2+, S = 2), and the corresponding spectra can be modeled in the frame of a S = 2 spin Hamiltonian accounting for a ligand field potential of low symmetry. The analysis of the spectra indicate that the principal axes (ξ,ς,ζ) of the electric field gradient tensor (EFG) are rotated with respect to the frame that defines the zero-field splitting. By assuming fast electronic relaxation, with the relevant and non-zero parameter values being set as given below (see article Table I), the corresponding theoretical curves calculated by MossWinn are quite close to those displayed on Figs. 4 & 5 of the above paper. Note that the small peak around v ≈ 3 mm/s — that shows up in Fig. 5 of the above paper for the 25 kG case — is neither confirmed by MossWinn nor by the experimental spectrum itself.

    Conversion factors to be considered in this example

    Vzz / 1021 V m-2 ≈ 6 × ½eQVzz / mm s-1

    D / cm-1 ≈ 0.69503457 × D / K

    Effective Hamiltonian (S = 2)

    Electronic states: μB[gxxBxSx + gyyBySy + gzzBzSz] +
    D[Sz2 – S(S + 1)/3 + (E/D)(Sx2 – Sy2)]

    Nuclear states: gnμN[Axx<Sx>TIx + Ayy<Sy>TIy + Azz<Sz>TIz] +
    [eQnVζζ/(4I(2I – 1))][3I ζ2 – I(I+1)+η(Iξ2 – Iς2)] – gnμN[BxIx + ByIy + BzIz]

    Case:

    Bext = 8.6 kG

    Bext = 25 kG

    Theory used:

    PHS Angle (Powder, EMF, Decoupled, Fast R.)

    (0) TEMPERATURE [K]:

    4.2

    (0) EXT. MAGN. FIELD [T]:

    0.86

    2.5

    (0) EMF PAR (0) / PERP (1):

    0

    (1) ISOMER SHIFT:

    0.82

    (1) Vzz (EFG) [10^21 V/m2]:

    13.2

    (1) ETA:

    0.8

    (1) D [1/cm]:

    13.9

    (1) E/D:

    0.15

    (1) Axx [T]:

    -18.0

    (1) Ayy [T]:

    -12.5

    (1) Azz [T]:

    -15.0

    (1) gxx:

    2.24

    (1) gyy:

    2.32

    (1) gzz:

    2.00

    (1) 2S+1 (multiplicity):

    5

    (1) Coupled (0) / Decoupled (1):

    1

    (1) Accuracy level:

    3

    (1) LINE WIDTH:

    0.25

    (1) THETA (EFG):

    70

    (1) PHI (EFG):

    60

S = 2

See Fig. 2 of Biochemistry 14 (1975) 4159.

  • In this example reduced chloroperoxidase is studied in various parallel applied magnetic fields at 4.2 K. Here we focus on the spectrum measured in a 25 kG external magnetic field. Heme iron is present in this reduced enzyme in the high-spin ferrous form (Fe2+, S = 2), and the corresponding spectra can be modeled in the frame of a S = 2 spin Hamiltonian. The analysis of the spectra indicate that the principal axes (ξ,ς,ζ) of the electric field gradient tensor (EFG) are rotated with respect to the frame that defines the zero-field splitting. By assuming fast electronic relaxation, with the relevant and non-zero parameter values being set as given below (see article Figure 2), the corresponding theoretical curve calculated by MossWinn is quite close to that displayed on Fig. 2 of the above paper.

    Conversion factors to be considered in this example

    Vzz / 1021 V m-2 ≈ 6 × ½eQVzz / mm s-1

    D / cm-1 ≈ 0.69503457 × D / K

    Effective Hamiltonian (S = 2)

    Electronic states: μB[gxxBxSx + gyyBySy + gzzBzSz] +
    D[Sz2 – S(S + 1)/3 + (E/D)(Sx2 – Sy2)]

    Nuclear states: gnμN[Axx<Sx>TIx + Ayy<Sy>TIy + Azz<Sz>TIz] +
    [eQnVζζ/(4I(2I – 1))][3I ζ2 – I(I+1)+η(Iξ2 – Iς2)] – gnμN[BxIx + ByIy + BzIz]

    Case:

    Bext = 25 kG

    Theory used:

    PHS Angle (Powder, EMF, Decoupled, Fast R.)

    (0) TEMPERATURE [K]:

    4.2

    (0) EXT. MAGN. FIELD [T]:

    2.5

    (0) EMF PAR (0) / PERP (1):

    0

    (1) ISOMER SHIFT:

    0.85

    (1) Vzz (EFG) [10^21 V/m2]:

    12.99

    (1) ETA:

    1.0

    (1) D [1/cm]:

    13.9

    (1) E/D:

    0.15

    (1) Axx [T]:

    -26.0

    (1) Ayy [T]:

    -12.0

    (1) Azz [T]:

    -15.0

    (1) gxx:

    2.24

    (1) gyy:

    2.32

    (1) gzz:

    2.00

    (1) 2S+1 (multiplicity):

    5

    (1) Coupled (0) / Decoupled (1):

    1

    (1) Accuracy level:

    3

    (1) LINE WIDTH:

    0.2

    (1) THETA (EFG):

    70

    (1) PHI (EFG):

    70

S = 2

See Fig. 4 of Inorganic Chemistry 48 (2009) 8317.

  • In this example the high-spin organoiron(II) complex Phenyltris((tert-butylthio)methyl)borate]Fe(Me) ( [C6H5B(CH2SC(CH3)3)3)]Fe(Me) ) is studied at various temperatures and external magnetic fields. Here we focus on the spectra displayed on Fig. 4 of this work. In the studied compound iron is present in the high-spin ferrous form (Fe2+, S = 2), and the corresponding spectra can be modeled in the frame of a S = 2 spin Hamiltonian. By assuming fast electronic relaxation and a parallel field direction, with the relevant and non-zero parameter values being set as given below (see article Table 4), the corresponding theoretical curves calculated by MossWinn appear to be identical with those displayed on Fig. 4 of the above paper.

    Conversion factor to be considered in this example

    A / T ≈ 0.725282 × A / MHz (for the ground nuclear level of 57Fe)

    Effective Hamiltonian (S = 2)

    Electronic states: μB[gxxBxSx + gyyBySy + gzzBzSz] +
    D[Sz2 – S(S + 1)/3 + (E/D)(Sx2 – Sy2)]

    Nuclear states: gnμN[Axx<Sx>TIx + Ayy<Sy>TIy + Azz<Sz>TIz] – gnμN[BxIx + ByIy + BzIz]

    Sample:

    Phenyltris((tert-butylthio)methyl)borate]Fe(Me)

    Theory used:

    PHS (Powder, EMF, Decoupled, Fast R.)

    (0) TEMPERATURE [K]:

    as indicated beside the spectra

    (0) EXT. MAGN. FIELD [T]:

    as indicated beside the spectra

    (0) EMF PAR (0) / PERP (1):

    0

    (1) ISOMER SHIFT:

    0.6

    (1) D [1/cm]:

    -33.0

    (1) E/D:

    0.01

    (1) Axx [T]:

    -7.25282

    (1) Ayy [T]:

    -7.25282

    (1) Azz [T]:

    24.51453

    (1) gxx:

    2.0

    (1) gyy:

    2.0

    (1) gzz:

    2.5

    (1) 2S+1 (multiplicity):

    5

    (1) Coupled (0) / Decoupled (1):

    1

    (1) Accuracy level:

    2

    (1) LINE WIDTH:

    0.35

S = 2

See Fig. 6 of Biochemistry 51 (2012) 8743.

  • In this example the 57Fe Mossbauer spectra of a high-spin ferrous complex (Fe2+, S = 2) designated as Y257FHPCAES were measured (among others) at 4.2 K in parallel external magnetic fields of various magnitudes. The corresponding spectra can be modeled in the frame of a S = 2 spin Hamiltonian. The analysis of the spectra indicate that the principal axes (ξ,ς,ζ) of the electric field gradient tensor (EFG) and those of the hyperfine magnetic interaction tensor (A) are rotated with respect to the frame (x,y,z) that defines the zero-field splitting. By assuming slow electronic relaxation, with the relevant and non-zero parameter values being set as given below (see article Table 3), the corresponding theoretical curves calculated by MossWinn appear to be identical with those displayed on Fig. 6 of the above paper. Note that the Euler angles related to the EFG and A tensors are used in MossWinn as the Euler angles that rotate the (x,y,z) system into the respective eigensystem of the EFG and the A tensors, whereas the authors refer to the corresponding angles as "the Euler angles that rotate the EFG- and A-tensor into (x,y,z)". For a description of corresponding Euler angles as used in MossWinn see section 27.6.7 in the manual.

    Conversion factor to be considered in this example

    Vzz / 1021 V m-2 ≈ 6 × ½eQVzz / mm s-1

    Effective Hamiltonian (S = 2)

    μB[gxxBxSx + gyyBySy + gzzBz Sz] + D[Sz2 – S(S + 1)/3 + (E/D)(Sx2 – Sy2)] + gnμN[S·A·I] + [eQnVζζ/(4I(2I – 1))][3I ζ2 – I(I+1)+η(Iξ2 – Iς2)] – gnμN[BxIx + ByIy + BzIz]

    Sample:

    Y257FHPCAES

    Theory used:

    PHS Angle (Powder, EMF, Slow R.)

    (0) TEMPERATURE [K]:

    4.2

    (0) EXT. MAGN. FIELD [T]:

    as indicated beside the spectra

    (0) EMF PAR (0) / PERP (1):

    0

    (1) ISOMER SHIFT:

    1.12

    (1) Vzz (EFG) [10^21 V/m2]:

    19.0

    (1) ETA:

    0.2

    (1) D [1/cm]:

    -11.2

    (1) E/D:

    0.32

    (1) Axx [T]:

    -22.0

    (1) Ayy [T]:

    -29.0

    (1) Azz [T]:

    -6.3

    (1) gxx:

    2.0

    (1) gyy:

    2.0

    (1) gzz:

    2.0

    (1) 2S+1 (multiplicity):

    5

    (1) Coupled (0) / Decoupled (1):

    0

    (1) Accuracy level:

    3

    (1) LINE WIDTH:

    0.33

    (1) THETA (A):

    6.5

    (1) PHI (A):

    98

    (1) GAMMA (A):

    76

    (1) THETA (EFG):

    27

    (1) PHI (EFG):

    160

S = 5/2

See Fig. 2 of BBA 264 (1972) 11.
or see Phys. Rev. B 5 (1972) 4257.

  • In this work the 57Fe Mossbauer spectrum model of LiFexAl5-xO8 (x = 0.005), at 4.2 K without the application of an external magnetic field, is given on the top of Fig. 2 as an example. The model corresponds to a high-spin ferric (Fe3+, S = 5/2) spin Hamiltonian. By assuming slow electronic relaxation, with the relevant and non-zero parameter values being set as given below (see article Fig. 2), the corresponding theoretical curve calculated by MossWinn (as shown on the right) agrees closely with that displayed on Fig. 2 of the above paper.

    Conversion factors to be considered in this example

    Vzz / 1021 V m-2 ≈ 6 × ½eQVzz / mm s-1

    A / T ≈ 8.431246 × A / mm s-1 (for the ground nuclear level of 57Fe)

    Effective Hamiltonian (S = 5/2)

    D[Sz2 – S(S + 1)/3] + gnμN[AxxS xIx + AyySyIy + AzzSzIz] +
    [eQnVzz/(4I(2I – 1))][3I z2 – I(I+1)]

    Sample:

    LiFexAl5-xO8 (x = 0.005)

    Theory used:

    PHS (Powder, ZERO EMF, Slow R.)

    (0) TEMPERATURE [K]:

    4.2

    (1) ISOMER SHIFT:

    0.3

    (1) Vzz (EFG) [10^21 V/m2]:

    4.0

    (1) D [1/cm]:

    -0.104

    (1) Axx [T]:

    -20.65655

    (1) Ayy [T]:

    -20.65655

    (1) Azz [T]:

    -20.65655

    (1) 2S+1 (multiplicity):

    6

    (1) LINE WIDTH:

    0.45

S = 5/2

See Fig. 11 of Biochemistry (Structure and Bonding) 20 (1974) 59.

  • On Fig. 11 of the above work theoretical curves are compared for crystal fields of rhombic and trigonal symmetry, by considering the cubic crystal field term (which includes the factor of a/6 in the Hamiltonian expression below) that introduces 4th order terms in the effective spin Hamiltonian. In the rhombic case the cubic axes (ξ,ς,ζ) coincide with the (x,y,z) axes of the axial term (i.e. axial distortion takes place along one of the cube axes). In the trigonal case the z axis of the axial term points in the <111> direction of the cube given by the cubic axes of (ξ,ς,ζ), i.e. the axial distortion occurs along the cube diagonal. Assuming a sample temperature of 4.2 K, an external magnetic field of 1.3 kOe applied perpendicular to the γ beam, as well as slow electronic relaxation, with the relevant parameter values being set as given below (see article Fig. 11), the corresponding theoretical curves calculated by MossWinn agree quite well with those on Fig. 11 of the above paper. Note, however, that in the rhombic case MossWinn produces a clearly smoother curve with respect to that given on Fig. 11, which we tend to associate with the higher accuracy of the numerical spherical (powder) integral routine built into MossWinn.

    Conversion factors to be considered in this example

    Vzz / 1021 V m-2 ≈ 6 × ½eQVzz / mm s-1

    A / T ≈ –14.768 × A / mm s-1 (for the excited nuclear level of 57Fe)

    Effective Hamiltonian (S = 5/2)

    μB[gxxBxSx + gyyBySy + gzzBz Sz] + D[Sz2 – S(S + 1)/3] +
    (a/6)·[Sξ4 + Sς4 + Sζ4 – (1/5)·S(S + 1)(3S2 + 3S – 1)] +
    gnμN[AxxS xIx + AyySyIy + AzzSzIz] + [eQnVzz/(4I(2I – 1))][3I z2 – I(I+1)] – gnμN[BxIx + ByIy + BzIz]

    Case:

    Rhombic <001>

    Trigonal <111>

    Theory used:

    PHS
    (Powder, EMF, Slow R.)

    PHS Trigonal
    (Powder, EMF, Slow R.)

    (0) TEMPERATURE [K]:

    4.2

    (0) EXT. MAGN. FIELD [T]:

    0.13

    (0) EMF PAR (0) / PERP (1):

    1

    (1) ISOMER SHIFT:

    0.0

    (1) Vzz (EFG) [10^21 V/m2]:

    -1.8

    (1) ETA:

    0.0

    (1) D [1/cm]:

    0.5

    (1) a [1/cm]:

    0.375

    (1) Axx [T]:

    -22.3

    -22.3

    (1) Ayy [T]:

    -22.3

    (-22.3)

    (1) Azz [T]:

    -22.3

    -22.3

    (1) gxx:

    2.0

    2.0

    (1) gyy:

    2.0

    (2.0)

    (1) gzz:

    2.0

    2.0

    (1) 2S+1 (multiplicity):

    6

    (1) Coupled (0) / Decoupled (1):

    1

    (1) Accuracy level:

    3

    (1) LINE WIDTH:

    0.3

S = 5/2

See Fig. 10 of Biochemistry (Structure and Bonding) 20 (1974) 59.

  • In this example, taken from the same article as the previous one, the effect of the rhombicity parameter λ = E/D on the spectral shape is illustrated via theoretical spectrum curves corresponding to a rhombic S = 5/2 spin Hamiltonian. Assuming a sample temperature of 4.2 K, an external magnetic field of 1.3 kOe applied perpendicular to the γ beam, as well as slow electronic relaxation, with the relevant parameter values being set as given below (see article Fig. 10), the corresponding theoretical curves calculated by MossWinn show fair agreement with those on Fig. 10 of the above paper, though some differences can also be observed mainly for λ = E/D = 0.0 in the central velocity range of -3 mms/s ... 3 mm/s. As in the previous case, we tend to associate the differences with the higher accuracy of the numerical spherical (powder) integral routine built into MossWinn. Note that on page 79 of the above paper a resolution of 100 orientations of the external magnetic field over one octant of the unit sphere is mentioned, which is higher than the case Accuracy = 1 in MossWinn (64 orientations over one octant), but is way below the case Accuracy = 2 (256 orientations over one octant), let alone cases Accuracy = 3 (1024 orientations over one octant) and Accuracy = 4 (4096 orientations over one octant) of MossWinn.

    Conversion factors to be considered in this example

    Vzz / 1021 V m-2 ≈ 6 × ½eQVzz / mm s-1

    A / T ≈ –14.768 × A / mm s-1 (for the excited nuclear level of 57Fe)

    Effective Hamiltonian (S = 5/2)

    μB[gxxBxSx + gyyBySy + gzzBz Sz] + D[Sz2 – S(S + 1)/3 + (E/D)(Sx2 – Sy2)] + gnμN[AxxS xIx + AyySyIy + AzzSzIz] +
    [eQnVzz/(4I(2I – 1))][3Iz2 – I(I+1)+3(E/D)(Ix2 – Iy2)] – gnμN[BxIx + ByIy + BzIz]

    Case:

    Rhombic Hamiltonian

    Theory used:

    PHS (Powder, EMF, Slow R.)

    (0) TEMPERATURE [K]:

    4.2

    (0) EXT. MAGN. FIELD [T]:

    0.13

    (0) EMF PAR (0) / PERP (1):

    1

    (1) ISOMER SHIFT:

    0.0

    (1) Vzz (EFG) [10^21 V/m2]:

    -3.0

    (1) ETA:

    3·E/D

    (1) D [1/cm]:

    0.5

    (1) E/D:

    as indicated beside the spectra

    (1) Axx [T]:

    -22.15195

    (1) Ayy [T]:

    -22.15195

    (1) Azz [T]:

    -22.15195

    (1) gxx:

    2.0

    (1) gyy:

    2.0

    (1) gzz:

    2.0

    (1) 2S+1 (multiplicity):

    6

    (1) Coupled (0) / Decoupled (1):

    1

    (1) Accuracy level:

    3

    (1) LINE WIDTH:

    0.45

S = 5/2

See Fig. 6 of Biochemistry 11 (1972) 3212.

  • In this example the 57Fe Mossbauer spectrum of PCA-4,5-oxygenase-protocatechualdehyde complex, taken at 4.2 K in a 150 G external magnetic field oriented perpendicular to the γ beam, is displayed on Fig. 6, along with a model curve based on a S = 5/2 rhombic spin Hamiltonian. Assuming slow electronic relaxation, with the relevant parameter values being set as given below, the corresponding theoretical curve calculated by MossWinn shows good agreement with that on Fig. 6 of the above paper.

    Conversion factor to be considered in this example

    Vzz / 1021 V m-2 ≈ 6 × ½eQVzz / mm s-1

    Effective Hamiltonian (S = 5/2)

    μB[gxxBxSx + gyyBySy + gzzBz Sz] + D[Sz2 – S(S + 1)/3 + (E/D)(Sx2 – Sy2)] + gnμN[AxxS xIx + AyySyIy + AzzSzIz] +
    [eQnVzz/(4I(2I – 1))][3Iz2 – I(I+1)+η(Ix2 – Iy2)] – gnμN[BxIx + ByIy + BzIz]

    Case:

    Rhombic Hamiltonian

    Theory used:

    PHS (Powder, EMF, Slow R.)

    (0) TEMPERATURE [K]:

    4.2

    (0) EXT. MAGN. FIELD [T]:

    0.015

    (0) EMF PAR (0) / PERP (1):

    1

    (1) ISOMER SHIFT:

    0.5

    (1) Vzz (EFG) [10^21 V/m2]:

    3.3

    (1) ETA:

    1.0

    (1) D [1/cm]:

    -0.7

    (1) E/D:

    0.33333

    (1) Axx [T]:

    -21.9

    (1) Ayy [T]:

    -21.9

    (1) Azz [T]:

    -21.9

    (1) gxx:

    2.0

    (1) gyy:

    2.0

    (1) gzz:

    2.0

    (1) 2S+1 (multiplicity):

    6

    (1) Coupled (0) / Decoupled (1):

    1

    (1) Accuracy level:

    2

    (1) LINE WIDTH:

    0.35

S = 5/2

See Fig. 9 of J. Phys. Chem. Solids 38 (1977) 883.

  • In this example the ferric hexaquo complex [Fe(H2O)6]3+ is studied in aqueous frozen solutions. The corresponding 57Fe Mossbauer spectra are modeled with a S = 5/2 spin Hamiltonian. The experimental data require the consideration of a cubic term. On Fig. 9 of the above paper, a series of model spectra are presented, which correspond to a rhombic crystal field term where the system of rhombic crystal field axes is rotated around the z axis with an angle of 45 deg with respect to the cubic (ξ,ς,ζ) axes. By assuming a sample temperature of 4.5 K along with slow electronic relaxation, with the relevant parameter values being set as given below (see article page 893), the corresponding theoretical curves calculated by MossWinn appear to be identical with those displayed on Fig. 9 of the above paper.

    Effective Hamiltonian (S = 5/2)

    μB[gxxBxSx + gyyBySy + gzzBz Sz] + D[Sz2 – S(S + 1)/3 + (E/D)(Sx2 – Sy2)] +
    (a/6)·[Sξ4 + Sς4 + Sζ4 – (1/5)·S(S + 1)(3S2 + 3S – 1)] +
    gnμN[AxxS xIx + AyySyIy + AzzSzIz] – gnμN[BxIx + ByIy + BzIz]

    Case:

    Rhombic Hamiltonian

    Theory used:

    PHS Angle (Powder, EMF, Slow R.)

    (0) TEMPERATURE [K]:

    4.5

    (0) EXT. MAGN. FIELD [T]:

    as indicated beside the spectra

    (0) EMF PAR (0) / PERP (1):

    1

    (1) ISOMER SHIFT:

    0.5

    (1) Vzz (EFG) [10^21 V/m2]:

    0.0

    (1) ETA:

    0.0

    (1) D [1/cm]:

    0.1

    (1) E/D:

    0.26

    (1) a [1/cm]:

    0.017

    (1) Axx [T]:

    -23.2

    (1) Ayy [T]:

    -23.2

    (1) Azz [T]:

    -23.2

    (1) gxx:

    2.0

    (1) gyy:

    2.0

    (1) gzz:

    2.0

    (1) 2S+1 (multiplicity):

    6

    (1) Coupled (0) / Decoupled (1):

    1

    (1) Accuracy level:

    3

    (1) LINE WIDTH:

    0.5

    (1) PHI (CFS):

    45

S = 0

See Fig. 1 of BBA 791 (1984) 244.

  • By setting 2S+1 to 1, and thus S=0, one can use MossWinn's PHS models to account for the case of diamagnetic iron, as well as cases where the hyperfine magnetic interaction can be neglected. Assuming that the application of the external magnetic field does not induce noticable effective hyperfine magnetic field, these also include cases of fast paramagnetic relaxation where the hyperfine magnetic field relaxes fast enough for its effect being averaged to zero. In this way the PHS model with S=0 also realizes an extension of the model of Blaes et al. (see NIM B 9 (1985) 201., named "Random EFG in uniaxial external magnetic field (Powder)" in MossWinn) for the case of a non-zero asymmetry parameter. Here we treat the case of diamagnetic Na2[Fe(CN)5NO]·2H2O (sodium nitroprusside) measured as control material in the above work at 4.2 K in 4 T external magnetic field oriented perpendicular to the γ-ray direction. With the relevant and non-zero parameter values being set as given below (see article Table II), the theoretical curve calculated by MossWinn (as shown on the right) appears to be identical with the corresponding curve in Fig. 1 of the above paper.

    Conversion factor to be considered in this example

    Vzz / 1021 V m-2 ≈ 6 × ½eQVzz / mm s-1

    Effective Hamiltonian

    [eQnVzz/(4I(2I – 1))][3I z2 – I(I+1)+η(Ix2 – Iy2)] – gnμN[BxIx + ByIy + BzIz]

    Theory used:

    PHS (Powder, EMF, Slow R.)

    (0) TEMPERATURE [K]:

    4.2

    (0) EXT. MAGN. FIELD [T]:

    4.0

    (0) EMF PAR (0) / PERP (1):

    1

    (1) ISOMER SHIFT:

    -0.19

    (1) Vzz (EFG) [10^21 V/m2]:

    10.22174

    (1) ETA:

    0.15

    (1) 2S+1 (multiplicity):

    1

    (1) Coupled (0) / Decoupled (1):

    1

    (1) Accuracy level:

    3

    (1) LINE WIDTH:

    0.24